数据科学的数学基础W1 课程概览向量与矩阵基础

阅读数: 次 2020-03-12

数据科学的数学基础W1:course overview/ 向量和矩阵基础

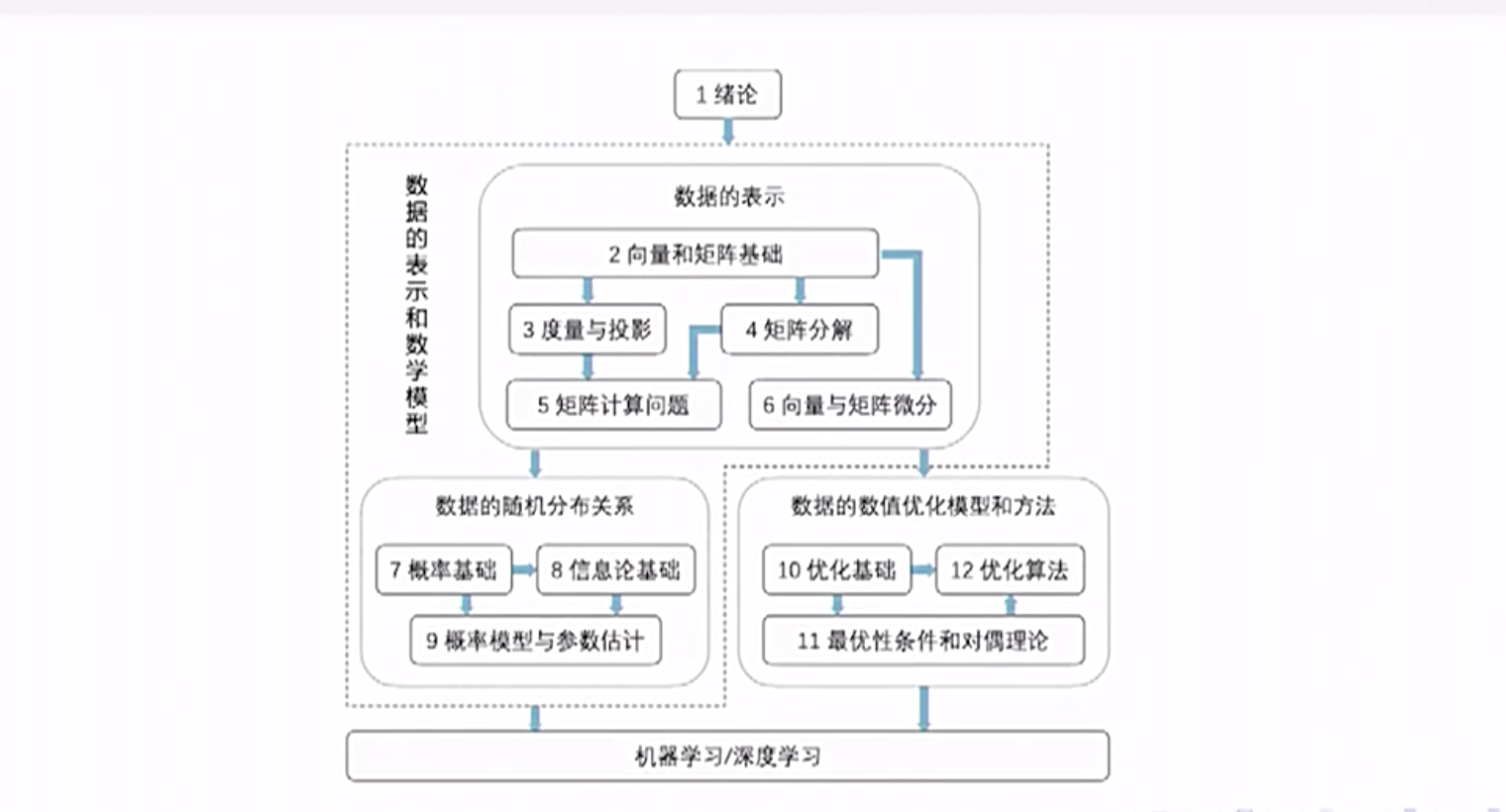
Course Outline

截屏2020-03-12上午9.14.37.png

ML：四个空间和三大函数的性质。

四个空间：输入空间、输出空间、特征空间、假设空间；

函数：线性函数、损失函数、目标函数；

Chapter 3.1 向量和矩阵基础数据

数据如何表示？

引例：词袋模型统计词频和图像的灰度存储

向量

定义

数域

包含0和1，且任意数的加减乘除也在该数集中。

数域K上的n维向量

数域K中的n个数组组成的有序数组。

约定

常用列向量来处理和表示

矩阵

灰度图像矩阵

词项-文档矩阵

总结

一元数组：向量
二元数组：矩阵
三元 及以上的高维：张量

例：可用m$$\times$$n$$\times$$3来表示
非数组型结构化目标：半群/群

当用向量进行了数据的表示之后，我们可以通过处理向量，来获得更好的潜在表示。

原始向量的低维近似：主成分分析和奇异值分解
原始向量的高维表示：特征映射构造，原始向量的高维表示的非线形组合。

jsonContent: meta: false pages: false posts: title: true date: true path: true text: false raw: false content: false slug: false updated: false comments: false link: false permalink: false excerpt: false categories: false tags: true